by Richard S. E. Keefe, PhD; Helena C. Kraemer, PhD; Robert S. Epstein, MD, MS; Ellen Frank, PhD; Ginger Haynes, PhD; Thomas P. Laughren, MD; James McNulty, AbScB; Shelby D. Reed, PhD; Juan Sanchez, MD; and Andrew C. Leon, PhD
Dr. Keefe is Professor of Psychiatry and Behavioral Sciences, Duke University Medical Center, Durham, North Carolina; Dr. Kraemer is with Stanford University (Emerita), Stanford, California, and University of Pittsburgh, Pittsburgh, Pennsylvania; Dr. Epstein is with Epstein Health, Woodcliff Lake, New Jersey; Dr. Frank is with the Department of Psychiatry, University of Pittsburgh School of Medicine, Pittsburgh, Pennsylvania; Dr. Haynes is with Eli Lilly and Company, Indianapolis, Indiana; Dr. Laughren is with Laughren Psychopharm Consulting, LLC, Rockville, Maryland; Dr. McNulty is Executive Director at MHCA/OASIS-RI, Providence, Rhode Island; Dr. Reed is with Duke Clinical Research Institute, Durham, North Carolina; Dr. Sanchez is Analyst, Ladenburg Thalmann & Co., New York, New York; and Dr. Leon was Professor of Biostatistics in Psychiatry at Weill Cornell Medical College, New York, New York.
Innov Clin Neurosci. 2013;10(5–6 Suppl A):4S–19S
In memoriam for our colleague, Andy Leon (1951–2012)
Funding: Funding for transcription and editorial services provided by the ISCTM.
Financial Disclosures: Dr. Keefe currently receives funding from, is a consultant to, or is a shareholder of the following companies: Abbvie, Akebia, Amgen, Asubio, Bioline Rx, Biomarin, Boehringer-Ingelheim, Department of Veteran Affairs, Eli Lilly Laboratories, EnVivo, Feinstein Institute for Medical Research, GlaxoSmithKline, Lundbeck, Merck, Mitsubishi, National Institute of Mental Health, NeuroCog Trials, Inc., Novartis, Otsuka, Pfizer, PsychoGenics, Research Foundation for Mental Hygiene, Inc., Roche, Shire, Singapore Medical Research Council, Sunovion, Takeda, and Targacept; Dr. Kraemer has no conflicts of interest relevant to the contents of this article; Dr. Epstein serves on the board of directors of Illumina, Aveo, and Proteus Digital Health; Dr. Frank is on the advisory board of Servier International and receives royalties from Guilford Press and the American Psychological Association Press; Dr. Haynes is an employee and shareholder of Eli Lilly and Company; Dr. Laughren receives funding from, is a consultant to, or is a shareholder of the following companies: MGH CTNI, NIMH, Naurex, Cerecor, EnVivo, Roche, Edgemont, Neuron, Zogenix, MedAvante, ERT, Johnson and Johnson, Shire, Corcept, Quinn Emanuel Urquhart & Sullivan LLP, and Ulmer and Berne LLP; Dr. Reed has no conflicts of interest relevant to the contents of this article; Dr. Sanchez has no conflicts of interest relevant to the contents of this article; Dr. Leon had no conflicts of interest relevant to the contents of this article.
Key words: Clinically meaningful effect, psychopharmacology drug trials
Abstract: Objective: This article captures the proceedings of a meeting aimed at defining clinically meaningful effects for use in randomized controlled trials for psychopharmacological agents.
Design: Experts from a variety of disciplines defined clinically meaningful effects from their perspectives along with viewpoints about how to design and interpret randomized controlled trials.
Setting: The article offers relevant, practical, and sometimes anecdotal information about clinically meaningful effects and how to interpret them.
Participants: The concept for this session was the work of co-chairs Richard Keefe and the late Andy Leon. Faculty included Richard Keefe, PhD; James McNulty, AbScB; Robert S. Epstein, MD, MS; Shelby D. Reed, PhD; Juan Sanchez, MD; Ginger Haynes, PhD; Andrew C. Leon, PhD; Helena Chmura Kraemer, PhD; Ellen Frank, PhD, and Kenneth L. Davis, MD.
Results: The term clinically meaningful effect is an important aspect of designing and interpreting randomized controlled trials but can be particularly difficult in the setting of psychopharmacology where effect size may be modest, particularly over the short term, because of a strong response to placebo. Payers, regulators, patients, and clinicians have different concerns about clinically meaningful effects and may describe these terms differently. The use of moderators in success rate differences may help better delineate clinically meaningful effects.
Conclusion: There is no clear consensus on a single definition for clinically meaningful differences in randomized controlled trials, and investigators must be sensitive to specific concerns of stakeholders in psychopharmacology in order to design and execute appropriate clinical trials.
Introduction
One of the most important questions that arises following a treatment study with positive results is “is the effect clinically meaningful?” This simple question may be answered very differently depending upon the perspective of the person who is addressing it and the circumstances under which the question is being asked. For instance, a clinician receiving information that a new treatment with few side effects is available that addresses a completely unmet need in his or her patients may feel that any statistically significant effect is enough to try the new medication with appropriate patients. On the other hand, health economists and payers may argue that if a drug does not produce a clear change in functionality or reduction in other health costs, the new treatment is not sufficiently beneficial to engender financial support. Patients themselves may have a very different set of criteria for what medications will have a clinically meaningful impact on their lives. Statisticians, regulators, family members, administrators, and investors all have very different views on what constitutes a “clinically meaningful effect,” yet all of these perspectives have an impact on the availability and use of new medications. This article provides various viewpoints on the definition of a clinically meaningful effect and how these varying perspectives influence treatment in central nervous system (CNS) disorders.
The effect of a treatment reflects the differential response among patients when treatment is given versus when treatment is not given (control/comparison condition, often placebo). Statistically significant effects are not necessarily clinically meaningful effects.[1] While there is broad consensus as to how to establish statistical significance, clinical significance remains elusive.
Many statistical methodologies have been put forth to measure the magnitude of a clinical effect (an effect size). One of the most frequently used effect size measures is Cohen’s d.[2] In a randomized controlled trial (RCT), Cohen’s d is the difference between the treatment and control means divided by the (assumed) common standard deviation. It is a clinically interpretable effect size, reflecting the degree of overlap between the patient responses in the treatment and control groups when the responses have normal distributions with equal variances.
Another commonly used example of an effect size is the success rate difference (SRD), which is related to the probability that a randomly selected patient from one treatment group (T1) has a response clinically preferable to that of a randomly selected patient from another group (T2). This is a number between -1 and +1, where +1 means that every T1 patient has a response clinically preferable to every T2 patient, -1 means the exact reverse, and 0 means equivalence of the two treatments. Where Cohen’s d is appropriate, d=2?(d/?2)-1. Thus there is a 1:1 (non-linear) correspondence between Cohen’s d and SRD when Cohen’s d is valid, but not otherwise. Another effect size is the number needed to treat (NNT), equal to 1/SRD. When the response is binary (success/failure), SRD is the difference between the success rates in T1 and T2, and NNT is the reciprocal of that success rate difference.
Despite the widespread familiarity of NNT among clinicians, how to interpret its magnitude in terms of clinical significance is difficult. For example, the NNT for low-dose aspirin regimens to prevent myocardial infarction has a high NNT of around 100, yet its prescription is common clinical practice. In general, when NNT is used to prevent relatively rare events, NNT is very high (poor) because most patients will not have that event whether in T1 or T2 groups. On the other hand, the NNT for certain psychotherapies to reduce symptoms of depression among those with major depressive disorder is about 3. Yet many doctors and patients and many studies find psychotherapy less effective in clinical practice than antidepressants. In this case, the NNT is low (good) because most patients experience at least some decrease in symptoms.
Moreover, the NNT of a given agent depends on the specific outcome evaluated: Atorvastatin has a low (good) NNT for reducing serum low-density lipoprotein (LDL) levels, but a high (poor) NNT for stroke prevention. Revenues for a drug may be taken as a reflection of a drug’s acceptance in the marketplace, but NNTs do not correspond to revenues. For instance, atorvastatin and infliximab have good NNT values and large revenues, but duloxetine, olanzapine, and donepezil have poor NNT values yet also produce large revenues.
What is very clear is that a clinically meaningful effect may depend on the nature of the condition being treated, the consequences of inadequate treatment, the costs and risks of the treatment, the vulnerability of the population, and other such factors. It must also depend on which outcome is of greatest interest and how that outcome is measured (dichotomization almost always makes NNT poorer) and somehow must take both the benefits and the risks of the treatment into consideration. The identification and measurement of meaningful clinical effects pose a multifaceted challenge, in that many stakeholders in our healthcare system would define “clinically meaningful effect” in different ways and require different methods of evaluating it. This article seeks to provide multiple perspectives on the definition of what constitutes a “clinically meaningful effect:” the patient, the payer, the clinician, the statistician, the healthcare economist, the investor, and the United States Food and Drug Administration (FDA).
The Patient’s Perspective
Healthcare consumers do not have a unified idea about what constitutes a clinically meaningful response to treatment with CNS drugs. In fact, they often vary in terms of their opinions on what are the most important symptom targets for treatment. Data from four focus groups (n=34) of well-educated individuals involved with mental health (both patients and family members) found that younger people had higher expectations and were more likely to seek a cure than older individuals. For patients taking three or more medications, the most prominent complaints were anxiety and depression, in that order. Symptoms such as anergia, anhedonia, and isolating behavior were viewed as problematic by respondents but less so by clinicians. The issues most patients cared about seem related to being able to live a normal lifestyle (e.g., they wanted relief from bad decision-making, the ability to work and earn an income, and better sleep).
The patient perspective is often overlooked in psychopharmacological therapy, where patients, who are obviously important in decisions about adherence, frame the meaning of response in terms of practical relevance to help them function in life rather than to alleviate their condition. In other words, patients emphasize quality-of-life (QoL) endpoints as the most meaningful to them. When the Hamilton Depression Rating Scale, the Young Mania Rating Scale (YMRS), Brief Psychiatric Rating Scale (BPRS), and other similar tools were explained to survey respondents, none thought they would be useful to them as individuals, although they stated these measures might be helpful in large-scale assessments, such as RCTs.
In this connection, it must be mentioned that laypeople generally do not understand the fundamental concepts underlying clinical research, such as NNT, null hypothesis, meta-analysis, or placebo response, and, as a result, do not clearly understand clinical research. The “therapeutic misconception,” first named three decades ago, describes the situation when participants in a clinical trial misunderstand the nature of a clinical trial to the point that they think the research protocol is designed to provide them with their most beneficial treatment rather than meet a research objective.[3] Patients may express concern about other topics they do not understand thoroughly, such as actions taken by the FDA after a drug has already been approved.
Thus, there is a bifurcation in the American healthcare system in that healthcare consumers typically seek short-term, identifiable benefits, such as symptomatic relief, while clinicians elevate clinical outcomes, such as serum cholesterol levels or A1C count or scores on multi-item tests often corresponding poorly to symptomatic relief. As a result, the results of RCTs can be ill-designed to guide clinical decision-making. Most patients as well as practitioners use their own personal experiences and observations to determine a clinically meaningful response. This situation can be particularly pronounced with patients suffering from mental illness, in that the life course of these individuals is heterogeneous and not thoroughly understood, and may be alien to some clinicians.
Patients with mental illness want improved QoL and functioning and the ability to have as normal a lifestyle as possible, although these outcomes are rarely the primary target for treatments undergoing a regulatory approval process. In order to assess whether interventions will make a positive difference to patients, it is important to evaluate psychosocial outcomes. Four main concerns arise: First, there are methodological challenges in studying psychosocial outcomes. Second, just as drugs that build muscle mass must be taken within the framework of an exercise program to be effective, behavioral interventions may be needed together with pharmacological treatment for optimal psychosocial effect.
It may also be that behavioral intervention is a better choice for some and pharmacological treatment for others. We need to apply personalized medicine algorithms to recognize which treatment is better for which patients. Third, psychosocial measures, including QoL measures, are inherently subjective. Ten patients may bring to the research 10 different notions of what factors are important to defining QoL, which itself can be a moving target given that improved QoL will lead naturally to more opportunities for success, but also to more possibilities for struggle and failure at a higher level.
Finally, there must be recognition that any treatment powerful enough to give benefit may also be powerful enough to cause harm, though not necessarily to the same patients. It is important to consider the harm:benefit balance in evaluating any treatment, whether in a RCT or in clinical decision-making. Again, personalized medicine approaches may refine the signal of risk and benefit to any individual. These are formidable challenges. However, our research must become more patient-centric or it will cease to be relevant.
The Payer’s Perspective
Much of the cost for treatment for many CNS disorders comes not from patients themselves, but from third-party payers, such as government health systems and insurance providers. Therefore, state and federal government representatives and insurance company representatives are often in the position of deciding which treatments should be paid for or reimbursed. These decisions have a great impact on how patients with CNS disorders are treated. Part of the decision-making process for government and insurance representatives is to determine whether a treatment has a clinically meaningful effect from the position of the payer.
Sir Ronald Aylmer Fisher (1890–1962) contributed much to statistics, including ANOVA (analysis of variance), Fisher’s exact test, and Fisher’s equation. In 1926, Fisher discussed setting the p-value at <0.05, but conceded the limit was arbitrary.[4] Today, p<0.05 is generally accepted to be statistically significant, but besides being an arbitrary limit, it does not necessarily align with clinical significance. Clinicians know well that results from an RCT can be statistically significant without being clinically significant and vice versa.
It may be more appropriate to speak of a clinically meaningful effect size, which has been defined as “the smallest difference (i.e., effect size) …that patients perceive as beneficial and that would mandate, in the absence of troublesome side effects and cost, a change in the patient’s management.”[5] It seems reasonable that our healthcare system should frame clinical significance in terms of the smallest effect that makes a difference to the patient. Attempts by payers to define clinical differences in these ways have relied on distribution-based models and anchor-based analyses.
Normative levels can sometimes be used to set clinical goals. A good example of this kind of distribution model occurred for treatment of hyperlipidemia. A statistical distribution of serum cholesterol levels among Americans was established, and patients were given the clinical goal of achieving scores in the 25th percentile, which is a serum cholesterol level below 200. In this case, what was essentially a statistical measure was translated into a clinical value. While this approach may facilitate simple-minded treatment decisions, it has weaknesses, especially since artificial dichotomization of continuous measures eliminates important information in an analysis and significantly reduces the statistical power available to detect a treatment difference. For example, if a patient started with a cholesterol level of 300 and reduced it to 210, he would “fail,” but someone who started with 201 and ended with 199 would “succeed.”
In anchor-based evaluations, a preselected measure is compared against a global scale, usually assessed by a physician. The goal is to correlate results, typically obtained via a questionnaire, to the global rating, which acts as the anchor. Specific survey responses are associated with specific clinical conditions. For payers, it is more complex: Payers use a definition of significance that identifies the smallest clinical difference that would mandate reimbursement for a particular technology.
Because payers are not a homogeneous group, they may bring several conflicting objectives to research. Payers may arrive at conclusions that conflict with statistical significance and/or clinical significance because they emphasize different outcome measures.[6] For example, an airline as payer may be very concerned with loss of workdays because workers follow a very specific schedule, whereas a payer associated with research scientists may not be as concerned with lost workdays because these type of workers are less likely to follow a set schedule and therefore may be able to make up lost workdays more easily. For that reason, it is difficult to make generalizations about how payers view clinically meaningful differences.
Payers often rely on bridging studies, which are a form of anchor-based interpretation that extend clinical trials findings into new areas of inquiry, such as estimates of associated cost. Some bridging studies aim to correlate the clinical effect of treatment in a study with direct and indirect medical costs. A bridging study that set the definition of the minimum clinical change that could be associated with a meaningful cost difference recently reported that greater adherence to diabetes drug therapy was associated with decreased hospitalization and could save almost $5 billion a year.[7] Similar studies have found that adherent patients have lower costs than nonadherent patients.[8] These kinds of studies can be conducted outside of the framework of an RCT and may encourage payers to invest in adherence initiatives, since all payers are interested in cost savings. Sometimes bridging studies can shed light on the complicated healthcare costs. In 2009, Zhu et al[9] conducted a bridging study that related the degree of dependency of an Alzheimer’s disease patient to treatment cost, which offered an important new way for payers and healthcare consumers to quantify these expenditures in a meaningful way with respect to disease progression.
Bridging studies may require specific refinements to provide insight relevant to payers. Hurley et al[10] evaluated long-term outcomes and costs of an integrated rehabilitation program for chronic knee pain and found a nonstatistically significant difference in costs—total health costs and social costs differed, but not to the point of statistical significance.[10] When outliers in this study were trimmed, the difference persisted but still remained statistically insignificant. When missing data were imputed, the difference became statistically significant. Cost imputation can be crucial in bridging studies, because cost studies inevitably fail to capture all of the relevant data. Imputation of data requires a rigorous methodology, but, when done properly, will more accurately reflect real-world costs.
Payers may also be interested in determining if the severity of a condition is associated with cost differences. If lower costs are associated with less severe disease, then an RCT could be designed to demonstrate how improvements in the condition affect cost. In such a case, a drug that could improve a condition from “severe” to “moderate” could be quantified as saving a specific amount of money. Examples in the literature are studies evaluating losartan on cognitive improvement as measured on the Mini-Mental State Examination (MMSE) in hypertensive patients,[11] cost of treating breast cancer by stages,[12] and the efficacy of donepezil on cognitive dysfunction in Alzheimer’s disease.[13] Such studies can be very convincing to payers.
Payers seek RCTs with economic outcomes, and if investigators do not provide them, payers will nevertheless try to derive them. One can make arguments for or against building in economic endpoints in RCTs (Table 1).
Costs may be captured in terms of cost minimization (i.e., does this intervention save money?) or using a cost-benefit or cost-per-life-year-saved (CLYS) or cost-per-quality-adjusted-life-year (CQALYS). During study design, investigators should examine the statistical power required to detect X difference in a clinical measure and then model the associated economic saving. Upon conclusion of the RCT, economic models can be constructed, such that for an X change in a specific clinical measure, one can expect Y change in dollars. This information can then be used to set up cost minimization or other cost models (CLYS or CQALY). While payers are heterogeneous, their methods for cost assessment are fairly uniform.
A clear evolution of evidence has occurred: From statistical evidence to clinical evidence and now to payer evidence. For payers, the underlying question remains: What is enough to create value? For payers, value is not the same as mechanism of action, pathway, or assumptions about meeting unmet needs. Payers remain unimpressed by new pathways or unmet needs if they lack cost data that can tie a particular treatment to a meaningful economic outcome. Reimbursement has changed dramatically in the past decade and will continue to change rapidly in the future. In today’s healthcare environment, payers are looking for relevant data on how specific interventions create value in meaningful ways.
The Healthcare Economist’s Perspective
Healthcare economists conduct cost-effectiveness analyses with two assumptions: 1) that resources are limited, and 2) that society wants to maximize health benefits.[14] An incremental cost-effectiveness ratio is defined as a numerator equal to the difference in costs between two treatments divided by a denominator equal to the difference in effects between two treatments. To compare incremental cost-effectiveness ratios across treatments for different diseases in different populations, common metrics of effectiveness must be used. Two frequently used measures are “life-years saved” (LYS) and “quality-adjusted life-years” (QALYs). This approach allows for the use of decision rules to identify therapies deemed to be “cost-effective,” such as those with incremental cost-effectiveness ratios less than $50,000 per QALY or $100,000 per QALY (although no standard threshold for cost-effectiveness has been established).
Cost-utility analysis (CUA) is a form of cost-effectiveness analysis that accounts for QoL differences and incorporates patient preferences, or utilities, for a set of health outcomes. Findings from CUAs are reported as the additional cost per additional QALY for an intervention relative to standard care. Since real-life QoL values vary over time and can fluctuate even in the short-term, QALYs represent the area-under-the-“quality-adjusted”-curve (AUC) across time.
Cost-effectiveness studies must consider the perspective of the analysis, the time horizon over which costs and benefits are measured, and the comparator or comparison treatment, which ideally ought to reflect the current standard of care. The standard of care is not always readily apparent in many areas, particularly when it comes to mental health interventions. A comparison treatment chosen by researchers may of course differ substantially from that chosen by community clinicians.
While the costs for the treatment of mental health disorders vary considerably based upon diagnosis, the majority of costs associated with the treatment of severe mental illnesses are paid by governmental entities. Private payers contribute relatively little to severe mental illness costs because private payers tend to be employers, and people with severe mental illness are often unemployed or under-employed with no insurance benefits. Medicare, Medicaid, and the Veteran’s Administration are the principal payers for Alzheimer’s disease and depression treatments; Medicaid is a principal payer for schizophrenia and substance abuse; and the Veteran’s Administration is the principal payer for posttraumatic stress disorder.
While the direct medical cost is often typically represented in the numerator of an incremental cost-effectiveness ratio, depending on the perspective chosen for the cost-effectiveness analysis, costs can be far more inclusive, particularly for mental healthcare. The effective treatment of mental illness can improve social security, reduce disability, boost productivity, alleviate stress on the judicial system, and strengthen families, all of which have associated cost savings. Certain treatments of mental illness may have high direct medical costs but offer a large societal benefit, such as increased safety in the community.
In cost-benefit analyses, all costs and effects must be expressed in monetary units. Their use is relatively limited in healthcare as many consider it distasteful to assign dollar values to human life. Nevertheless, in mental health where successful treatment may produce cost savings throughout society (e.g. lower costs to the judicial system, disability payments, lower crime rates), a cost-benefit approach representing a societal perspective may be useful even if QoL benefits are not monetized. An advantage of cost-benefit analyses is their relative simplicity for interpreting results; if the benefits (B) exceed costs (C), i.e. if B>C, then the intervention should be implemented. If multiple interventions are available, the intervention with the highest benefit-to-cost ratio is preferred.
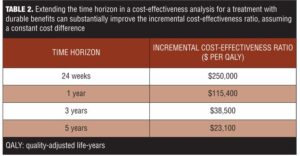
It is important to recognize that cost-effectiveness analyses and cost-benefit analyses typically require a number of assumptions. The following example demonstrates the importance of assumptions made about the duration of effectiveness of a treatment. In principle, the time horizon for a cost-effectiveness analysis should be long enough to capture all potential downstream costs and health consequences. To begin, we assume equal effectiveness for two interventions (Treatments T1 and T2) over a 24-week period. With equal effectiveness and no differences in adverse events, the analysis is limited to a cost comparison, also known as a cost-minimization analysis. The cost assumptions are that Treatment T1 costs $100 per week, while Treatment T2 costs $25 per week. The results of this analysis indicate that Treatment T2 is preferred because it is less costly. When one treatment is more effective than its comparator, a cost-effectiveness analysis is appropriate. In this scenario, response rates are 40 percent for T1 and 30 percent for T2 with no adverse events for either treatment and no extended benefits after the 24-week study concluded. If we assume that responders have a utility (QoL) equal to 1 and nonresponders have a utility (QoL) equal to 0.844, the incremental gain in QALYs with Treatment T is 0.0072. When combined with an incremental cost of $1800, the incremental cost-effectiveness ratio works out to about $250,000 per QALY (see calculations below):
QALYTrxT1=[(0.4 x 1)+(0.6 x 0.844)]*(24/52)=0.4183
QALYTrxT2=[(0.3 x 1)+(0.7 x 0.844)]*(24/52)=0.411 ? = 0.0072
Incremental Cost-Effectiveness Ratio=($2400-$600)/0.0072= $250,000 per QALY
An incremental cost-effectiveness ratio of $250,000 per QALY is far from what is considered cost effective. However, by extending the time horizon—that is, if the duration of effectiveness varies such that the benefit can be maintained for five years at the same incremental cost— the incremental cost-effectiveness ratio decreases markedly (Table 2).
Other factors that can affect cost-effectiveness results include the study design and the use of enriched patient populations—that is, patient groups that are assumed to show the greatest benefit (i.e., a larger denominator). Of course, cost-effectiveness studies have been criticized because they do not account for other factors considered in coverage decisions, such as equity, disease severity, and the rule of rescue. For that reason, multicriteria decision analysis is gaining interest because it allows decision makers to rationally consider several criteria.[15]
Thus, the cost-effectiveness of an intervention depends on multiple and sometimes interrelated factors: the effect size, the comparison (placebo or active comparator), the disease severity, the time horizon, and the perspective (e.g., whether the analysis incorporates data on employment, informal caregiving, use of medical resources, and impact on the judicial system).
The Investor’s Perspective
Wall Street is an important player in American healthcare, although it may be argued that stock analysts do not understand the nuances of RCTs and the clinical ramifications of study results. Investors take a very pragmatic view of medical research, because their intention is to make capital allocation decisions rather than to treat patients. Analysts favor benchmarking, a type of analysis that relies on precedents because it permits evaluation of a clinical study without necessarily having to delve into all of the clinical implications of the study results. For instance, if a pain reliever that improves pain by a specific unit X is both reimbursed and frequently prescribed (precedent), then investors can benchmark a new drug that relieves pain >X with a similar safety profile and know the new drug will be successful in the market. Benchmarking is most accurate when there are many precedents; however, in drug development, investors often face situations where there are few or no precedents.
Investors must consider the intervention within the context of the marketplace, which is constantly changing in terms of what is considered clinically meaningful, the range of competitive offerings that are available or in development, the availability of generics, and economic factors. Wall Street uses different metrics for assessing drugs, depending on where the product is in the approval process. For example, early in the regulatory process during the proof-of-concept phase, Wall Street will look at statistical analyses to determine the drug’s potential clinical significance, although it is not clear if their interpretation of results will be swayed by traditional misconceptions of p-values and effect sizes as described above. As the drug nears the end of its approval phase, investors start to think along the lines of the FDA (i.e., they run risk-benefit analyses). Investors are very familiar with FDA procedures and may know panelists reviewing drugs.
Investment decisions are made on the basis of long-term commercialization of the drug. Marketplace behavior is measured in revenues. For investors, quite bluntly, the meaningfulness of the clinical effect of a drug can be stated in terms of how many people are willing to buy it.
When benchmarking of a novel CNS product is difficult to impossible, investors may rely on responder analysis rather than comparisons. Responder analyses provide more information than mean-difference analyses, but they depend on a clear definition of response, which is typically defined based on regulatory considerations or to reduce variability. Such constricted definitions of response may actually reduce or preclude the demonstration of a clinically meaningful effect. Investors prefer functional endpoints, such as activities of daily living or QoL, over more “confusing” clinical endpoints, as the relevance of functional endpoints to everyday life and their ability to drive revenues is more clear. Co-primary endpoints that provide relevance for decisions to maintain treatments over time are also valued by investors. Finally, even without available benchmarks, investors rely heavily on key opinion leaders (KOLs) to endorse or reject new products. Products with enthusiastic backing by KOLs may be able to overcome modest clinical trial results; the reverse can also be true.
Clinical researchers tend to think that investors are interested in products with a new mechanism of action or a novel route of administration. While such products may have strong face value, the safety advantage has to be strong, relevant, and measurable in order to impress investors.
The marketplace reveals many examples of how investors have evaluated new drugs. Ampyra was a new drug with no precedents for benchmarking. Despite RCT endpoints that confused investors in terms of its clinically meaningful effect, Wall Street was impressed by the strong positive response from KOLs. The drug was approved and has been very profitable. On the other hand, viladozone was a drug that was relatively easy to benchmark and offered a potential new safety advantage; the drug has been approved but it is unclear how profitable it will be. A more puzzling drug is droxidopa, currently under consideration for the indication of neurogenic orthostatic hypotension. There are no precedents for benchmarking and studies center around a symptomatic endpoint (dizziness), which requires a comparison of means of unknown clinical relevance. Droxidopa is an interesting product and it is unclear if the drug will be financially successful.
Investors are interested in more than just drugs; they are interested in how companies perform after a drug is launched and while that drug is on the market. Many CNS drugs are not doing well, in that drugs with revenues of $80 or $90 million may notjustify the investment it took to produce them. Recent controversies about the overall efficacy of CNS drugs have heightened concern about these agents. Investors are, by nature, risk averse, and this positioning poses a conundrum for innovation in drug development. Innovative drugs carry more risks and are difficult, even impossible, to benchmark. But if Wall Street does not help support innovation in drug development, who will? It is unrealistic to assume that the government will take the lead in drug innovation.
Right now, disappointing revenues for certain CNS agents and decreasing company valuations are the natural outcome of having made investments based on the lowest degree of risk, but this downward trend will self-correct. Greater rewards are associated with greater risks. Wall Street investors follow the CNS drug market very closely, and while they may not always define clinically meaningful effects the way clinicians do, they understand the potential value of important new CNS products.
The FDA’s Perspective
The FDA looks for “substantial evidence” that a drug will do what it is labeled to do, although it does not define substantial evidence. There are no specific regulations defining minimum effect size or how to determine a clinically meaningful effect. There are no legal requirements, which set forth that a new agent has to be more effective than currently available agents, but sometimes, particularly in cases where there is a high risk of mortality or irreversible morbidity, the FDA will require a new drug to be at least as effective as currently available treatments to be approved. Effect size relative to other drugs can also play a role when currently available drugs are associated with a serious risk.
In the case of psychopharmacological agents, the FDA usually does not look at the principle of relative efficacy because mortality or irreversible morbidity are generally not at stake. In some cases, noninferiority analyses can be used to evaluate new drugs, but these are only applicable when the treatment effects are predictable, which may not often be the case with psychopharmacological drugs. The high and widely variable placebo response observed in psychiatric drug trials can result in a noninferiority margin of zero (i.e., no difference between the active drug and placebo).
Thus, CNS drugs often rely on superiority trials, which can be conducted with a placebo (easier) or active comparator (more difficult). Even for placebo studies, the placebo effect can make trials difficult, in that certain RCTs may find that an agent is no better than placebo, when, based on many other trials, the drug is considered to be an effective treatment.
Thus, approaches to determine efficacy of CNS drugs in RCTs should find ways to measure response and determine boundaries between responders and non-responders. The challenge in this paradigm is that response must be well defined, with clear criteria and easy metrics. There are many ways to define response. A particularly useful one in this context is to factor in long-term response (i.e., a responder counts only if the drug’s effect is durable). A standard rating scale can be used with response defined as a specific reduction on that scale—say, a 50-percent reduction on the Hamilton Depression Rating Scale (HAMD). While such response definitions can be clinically meaningful and are frequently used, they are arbitrary and there is no universal agreement as to what constitutes a clinically meaningful response. In addition to establishing a percentage reduction (or improvement) on a validated scale, a threshold value should be set.
A common approach in psychiatric drug evaluation, and one with which the FDA is comfortable, involves focusing on an illness-severity measure and then determining efficacy based on a change from baseline. There is no established value for what constitutes the minimum required effect size, although new guidance from the National Institute for Health and Clinical Excellence (NICE) in the United Kingdom has proposed that there should be a decrease of at least three measured HAM-D units to achieve a clinically meaningful effect.[16] Treatment response for psychiatric drugs are modest, but measurable, and many fall below the newly proposed NICE guidance, in that FDA estimates them to be around 2.5 HAM-D units, at both United States and international study sites. Furthermore, even the NICE threshold is still an arbitrary value.
Effect size is usually measured by regulators as the difference between the drug and placebo mean change from baseline using a standard measure. Cohen’s d would be the [(mean test group)-(mean control)]/standard deviation. While Cohen defined large, medium, and small effects as d=0.8, 0.5, and 0.2, respectively, an FDA rule of thumb is that an effect is deemed large if it is >0.8, small if it is <0.5, and moderate if it falls between those values. On the NNT scale then, large would be <2, small would be >4, and moderate if it falls between those two values.
Short-term studies do not always show large effects; this is particularly true in studies of antidepressants. Larger effect sizes are evident in maintenance trials, where 13 out of 13 trials for antidepressants produced positive results; the average difference in relapse rate between drug and placebo groups is about 20 percent (range 10–33%). It could be argued that these findings are more meaningful than short-term trial results because of the recurrent nature of depression.
As briefly described in the introduction above, the NNT value—how many people need to be treated with the new drug rather than placebo for one additional patient to benefit—can also be helpful to regulators. This can be calculated by defining the absolute risk reduction (ARR) as the number of people who respond to new drug minus the number who respond to placebo and using its reciprocal (1/ARR). For example, if response to the new drug is 50 percent and placebo response is 25 percent, then the ARR is 25 percent (50–25%) and the NNT is 4 (1/25%). Overall, the NNT is a meaningful, well-accepted, common-sense measure, but its value depends on how response is defined.
Like many other divisions at the FDA, the Division of Psychiatric Products (DPP) relies heavily on p-values and has not formally defined minimum effect size. However, when approval is based on a noninferiority analysis, it may be required to preserve a certain fraction of an established benefit and to meet a required effect size, e.g., thrombolytics. Other exceptions that may require a defined effect size include studies with mortality endpoints and studies involving weight loss drugs, which have a clear effect size in terms of the amount of pounds lost (since this effect is clinically interpretable, effect size makes sense here).
Finally, it should be noted that the FDA encourages functional endpoints as secondary endpoints in RCTs of psychiatric drugs using cognitive improvement variables as primary endpoints. These functional endpoints can even be included in the hypothesis as a key secondary endpoint and could result in labeling for an additional benefit.
Clinically Meaningful Similarity
In defining a clinically meaningful effect, it is important to know when the difference between treatments is small enough that it may be considered similar. The determination of a clinically meaningful similarity depends on the hypothesis of the study. The hypothesis of a noninferiority trial is fundamentally different from that of a superiority trial. A noninferiority trial must set boundaries for the noninferiority margin, which poses a challenge in terms of sample size.[17] Comparative effectiveness research (CER) compares the benefits and harms of different interventions and strategies that diagnose, treat, and monitor health conditions in real-world settings. Clinically meaningful similarity compares different active agents in terms of benefits and harms and determines “how close is close enough?”
CER may evaluate agents in terms of superiority (i.e., is the investigational agent superior to the active comparator?) In such cases, the null hypothesis is that the investigational agent is the same as the active comparator, while the alternative hypothesis is that the investigational agent is not the same as the active comparator. If a study results in failure to reject the null hypothesis, this might mean both treatments are effective, neither treatment is effective, or the study was insufficient (poor design, inadequate power). When conducting superiority evaluations, the degree of difference is usually not addressed; superiority spans all degrees of difference.
On the other hand, the objective of a noninferiority study is to determine if the investigational agent is worse than the active comparator. The null hypothesis is that the active agent is better than the investigational agent by at least a predefined noninferiority margin (the active agent minus the investigational agent ? noninferiority margin). Since the standard of care is often a generic drug, the research question behind most noninferiority studies is whether an inexpensive generic is inferior to a new and more costly drug. The alternative hypothesis is that the difference between the active and investigational agents is less than the noninferiority margin (i.e., the investigation agent is not inferior to the comparator).
The noninferiority margin or delta value must define the largest difference that is clinically indifferent. Changes measured on a validated scale or response rate are often the units for noninferiority margin, with investigators using the differences between active agents and placebo determined in meta-analyses to establish the margin. While the use of meta-analyses is recommended, such studies may not exist for new agents. The noninferiority margin should be less than the smallest effect of the active agent versus placebo and less than the clinically meaningful difference of superiority established by RCTs. Moreover, the noninferiority margin must be stated in the study protocol.
An example of a noninferiority margin can be taken from a meta-analysis of placebo-controlled RCTs for second-generation antipsychotics (SGAs) for treating schizophrenia.[18] If the standard deviation (SD) on PANSS is 20, then the delta value is 0.50 or 10 PANSS units. If five PANSS units correspond to noninferiority, then the delta value is 0.25. While this may be a common sense approach to the statistics, it is less clear whether this finding represents a clinically acceptable difference. There is very little guidance in the literature as to what constitutes a clinically acceptable difference, so it is useful at this juncture to involve clinicians and patients, and essential to engage regulators for Phase III studies.
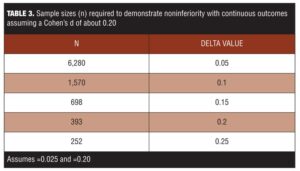
Noninferiority studies are not always practical because they demand a large sample size, much larger than generally required for superiority RCTs, even when the critical effect size is exactly the same in both. If the noninferiority margin is half of the difference expected in a superiority RCT, the noninferiority sample size must be four times larger (Table 3). Such trials may be cost prohibitive to their sponsors.
Assay sensitivity must be considered when two agents are found to be within the predetermined margin for clinical similarity. Measurement of clinical significance may be correctly attributed to efficacy, or there may be other factors involved. Some regulatory bodies recommend adding a placebo arm to studies to help better define efficacy. Noninferiority trials can be difficult to analyze when the active comparator separates inconsistently from the placebo, which essentially means noninferiority trials are not going to be useful for depression and anxiety drugs. If a noninferiority trial is used for a psychiatric drug, there must be a rigorous methodology in place to prevent spurious findings.
While noninferiority trials are not always appropriate in psychopharmacology, they are sometimes used and have presented interesting results. When conducting such a noninferiority trial, it is important to choose an appropriate noninferiority margin (delta value) that is small enough to be convincing to researchers and clinicians. Such noninferiority trials must have sound design, rigorous methodology, control for assay sensitivity, and have sufficiently large patient populations.
Determining How Effective a Treatment will be for an Individual Patient
The value of clinical research is the degree to which it improves the impact of clinical decision-making for an individual patient. Any study that approaches a research problem in this way—how can we improve decisions for an individual patient?—is likely to be more powerful, more cost effective, and have a greater impact on patient care. The primary objection to tackling research this way is that it differs from the way we have done things in the past. But this new paradigm brings with it a definite advantage, namely that it does not require large sample sizes or complex study designs.
Paul Meehl held that all null hypotheses of randomness are false, in that with a large enough sample size and sufficient number of RCTs, there will eventually result one or two more values of p<0.05.[19] A p-value less than the conventional 0.05 means that the sample size was large enough to detect some deviation from the null hypothesis, not that the deviation was clinically significant or important. A nonstatistically significant result means that the sample size was not large enough, and often reflects the adequacy of the study design in terms of sample size and units measured. Jones and Tukey also rightly criticized the null hypothesis.[20] Expanding the sample size, even to 10,000 patients or more, allows the investigators to get p-values far less than 0.05 even for treatment effects that are trivial. If two separate RCTs with p<0.05 were to mean approval of a drug, it would take only 40 RCTs to approve a drug absolutely equivalent to a placebo, and if each trial were run at the 80-percent power level, whatever the true effect size, it would take only about three. This means that those with deep enough pockets can eventually get their desired results; essentially anything can be approved with the right number of studies of large enough size. So if we know that the null hypothesis is never true, why do we as a healthcare system devote so much time and money trying to prove it is not?
Instead, attention should be focused on effect sizes—a population parameter (estimated in a sample) that indicates the potential clinical importance of a finding. In an RCT, the effect size and 95-percent two-tailed confidence interval (CI) should be reported; for a meta-analysis of several RCTs, using such effect sizes will provide a constantly shrinking CI, to the point that it falls either above the threshold (warranting drug approval) or below the threshold (denying drug approval). Furthermore, this methodology offers sponsors a cost advantage in that if values trended low enough, drug companies could stop investing in further trials.
As described briefly in the introduction above, the SRD offers a quantifiable probability based on whether the random selection of one patient from T1 and one from T2 will result in T1 clinically preferable to T2. This analysis is easy to compute, clinically meaningful, and converts easily into NNT (1/SRD), a familiar metric for clinicians.
At issue here is not whether that (or any other) effect size is the best choice, but rather how any effect size is interpreted in terms of clinical significance. The effect size depends on comparing the response in the two groups, but the interpretation depends on the consequences of not treating the patient and patient population. Thus what magnitude of effect size is considered clinically significant will vary widely from one indication to another, from one population to another, and from one outcome measure to another. Investigators must be able to articulate the principles behind clinical effect size definition rather than simply stating a number.
Effect size may indicate the average effect over the entire patient population sampled, or it may be the effect size for the typical person in that population. In either case, the effect size may not describe what occurred in any individual patient, but only either an average or that in a selected patient, both possibly misleading. For example suppose the study population were made up of equal numbers of men and women, where treatment T1 is better for women and treatment T2 is equally better for men. The average clinical effect is zero. The nonexistent “typical patient” is halfway between the women and men and is also zero. Yet there is a strongly preferred treatment here for everyone in the population.
For that reason, it is important to consider moderators—those baseline factors that identify subpopulations with different effect sizes. Moderators are a first step toward achieving the elusive goal of personalized medicine. In the previous example of men and women treated with T1 and T2, the moderator is gender. A baseline factor is considered a moderator (M) of the treatment (T) on the outcome (O) if the effect size of T on O changes depending on the value of M. The MacArthur model21 criteria for moderators aids in implementation of the following:
• There must be temporal precedence of M before T before O.
• M and T are not correlated.
• The effect size of T on O changes, depending on M.
The first two criteria are satisfied by any baseline variable (prerandomization) in an RCT.
The Multimodal Treatment of ADHD (MTA) study evaluated behavior therapy, medications, and their combination in the treatment of pediatric attention deficit hyperactivity disorder (ADHD) patients (ages 7–9).22 Patients were randomly assigned to one of four treatment arms: intensive medication management alone; intensive behavioral treatment alone; a combination of medication and behavioral treatment; or routine community care, which served as the control group. The outcome measure was a binary metric described as “excellent response.” Using recursive partitioning, it was found that a key moderator was parental depression. In the MTA study, the NNTs comparing pharmacological treatment versus TAU or behavioral treatment were 2.6 for children of nondepressed parents compared to 7 for children of depressed parents suggesting that the treatment (here a pharmacological treatment) was far more effective in patients with nondepressed parents. This type of exploratory analysis must be done with extreme care, as false positives may occur. In this particular case, parental depression had been identified in other studies as contributing to ADHD in children.
While there are many baseline factors to consider when comparing T1 to T2, there will only be a few real moderators of treatment on outcome. Hypothesis generation studies help to explore the possibilities, which must be sifted carefully in order to identify the true moderators. These explorations can be taken as rationale and justification for new hypotheses, but should not be considered conclusive. The search for moderators can result in surprises for investigators, both in what moderates and what does not. RCTs are often designed to control and adjust for a myriad of factors, but most of these factors will turn out to be irrelevant to the outcome and wind up costing the study power. The identification of a single moderator may not make a vast improvement in clinical decision-making processes, but decision rules based on multiple moderators bring us closer to personalized medicine.
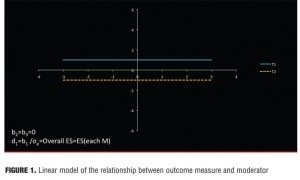
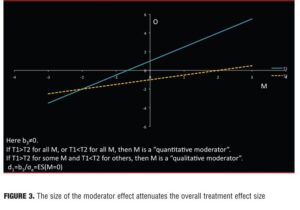
Recursive partitioning was employed in the MTA study, but a linear model also often works well and is more straightforward: 0=b0+b1T+b2M+b3TM+e (centering: T coded +1/2 and -1/2, M standardized to a mean of 0 and variance 1) where T indicates choice of treatment and M the proposed moderator. Then d0, d1, d2, and d3 are the standardized regression coefficients. A statistically significant interaction (b3 or d3) would document that M is a moderator. Under this model, the linear model relationship between outcome measure and moderator is depicted as a straight line (Figure 1).
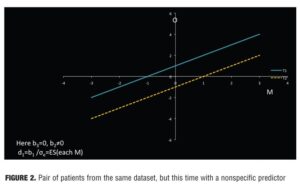
The separation between the lines and M indicates the effect size for that patient. In Figure 1, M is irrelevant to treatment outcome, for M is not associated with outcome in either treatment (flat lines), and the treatment effect is the same for all patients. In Figure 2, M is a nonspecific predictor. Here M is associated with outcome in both treatments (non-zero slope), but the effect size is the same for all patients (parallel lines.) In Figure 3, M is a moderator of treatment on outcome. M is associated with outcome in one or both groups, but the two lines are not parallel. Because the lines cross within the range of M, for some patients T1 is preferred to T2 and for others T2 to T1.
When using moderators, a moderator effect size is needed to compare and convey the potential impact of various moderators.
The overall treatment effect size (Cohen’s d) of T1 versus T2 can be expressed as follows: ES=d1/?(d22+d32/4+1),where d1 is the Cohen’s d for subjects with M=0. This clearly shows the attenuation in the magnitude of ES1 due to d2 and/or d3. The nonspecific effect size (NspES) is d2/?(d22+d32/4 + 1) and the moderator effect size (ModES) is (d3/2)/?(d22+d32/4 + 1), resulting in an overall effect size of d1 (1-NspES2-ModES2). These exercises shed some light on why the effect size in psychopharmacology may be so low: Unrecognized moderators will almost inevitably attenuate the overall effect size. It may be that with many CNS agents, effects are attenuated in ways not yet fully elucidated.
The easiest way to calculate moderator effect size is to pair each patient in T1 with each patient in T2. For each pair, compute the difference in outcome (delta-O) and the average of their moderators (AM). Then the correlation of delta-O and AM over all possible pairs is the estimate of the ModES.
It is not useful to have too many moderators in an analysis, so it is important to exclude from consideration those that are not well measured, may be redundant, or do not make sense. For each moderator, we might estimate the moderator effect size and its CIs by bootstrapping and then compare the effect sizes of the various moderators. A multiple regression analysis of paired differences on the averages of the moderators will result in a system of raw weights that may be applied to the data to generate the optimal moderator. Use multiple regression with the delta-O from all possible randomly paired subjects with independent measures of AM1, AM2, and so on as predictors, resulting in weights (W1, W2, and so on) arriving at the optimal moderator as M*=?wjMj. After calculating its effect size and CI, independent verification should be sought.
When analyzing data, it is important to determine clinically meaningful effect sizes and their confidence levels and to use moderators in RCTs and for clinical decision-making, knowing that these moderators can attenuate effect sizes. When using exploratory data analysis to identify individual moderators and their effect sizes and arrive at an optimal moderator (with its effect size), recognize that this is a foundation to hypothesis testing rather than a substitute for it. Independent verification is crucial.
These relatively straightforward techniques may change the direction of subsequent clinical research because they might better focus on moderated subgroups. This is a new way of thinking about research, but one that may allow us to get more targeted results and more closely approach our goal of personalized medicine.
What is crucial to all this is the availability of a single high-quality outcome measure that incorporates the considerations most important to a particular audience. It may well be that the outcome measures most important to clinicians and patients may be different from that to payers or policy makers, which, in turn, may be different from investors or from basic scientists. However, what is needed is a single measure for each audience.
Incorporating Risk and Benefit
Clinical research depends on a reliable, valid, and sensitive outcome measure (O), which is sensitive to crucial differences in treatment response among patients, better known as harms and benefits. As noted above, what is “crucial” may be different among clinical researchers, clinicians, patients, payers, and policy makers. For optimal study results, it is useful to express harms and benefits as a single outcome measure. Currently, medicine tends to separate measures of harm (collateral effects) and measures of benefits (efficacy), but this separation may result in an incomplete picture of clinical outcomes. Examples of this might be selective serotonin reuptake inhibitors (SSRIs) in youth (effective but with risk of suicide) or atypical antipsychotics (effective but with metabolic side effects). Our current approach to RCTs with multiple outcomes considered separately does not always allow us to determine if benefits and harms accrue in the same individuals. When benefits and harms are reported separately, it cannot be determined if T1>T2, T1=T2, or T1<T2 because crucial statistical and clinical information is missing. If investigators can accurately consider the effect of plural impacts (harms and benefits) on individual patients, this may lead them to draw different clinical conclusions.
Illustrating this point are data from a long-term maintenance trial of patients with recurrent depression who responded to combined short-term treatment with imipramine (IMI) and interpersonal psychotherapy (IPT).[23] In the three-year maintenance trial, patients were randomized to one of three groups: IMI, IPT plus medication (IPT-M), or medication clinic plus placebo (MC+PBO). The outcome measures were determined as follows:
• Benefit meant the patient completed the three year trial with no recurrence (binary outcome B = yes, b=no)
• Harm meant the patient experienced a side effect (dry mouth, constipation, diarrhea, sexual difficulties, clumsiness, poor coordination, difficulty speaking, nausea, or vomiting) for 1 month or longer causing significant distress or incapacity (binary outcome H = yes, h = no).
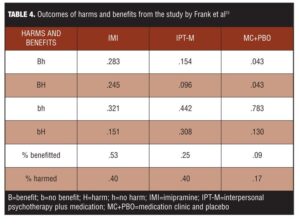
Using outcomes defined in this way, there were four possible outcome results for the three treatment groups (Table 4).[23]
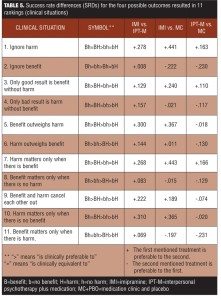
The study was designed so that patients were dropped from the study if they experienced a recurrence of depression, which means some left the trial before harm or benefit could accrue. Note from Figure 4 that about half of the population benefits from IMI, but 40 percent were harmed. In the IPT-M group, harm occurred at a rate of 40 percent. The correlation between benefit and harm is positive for IMI as well as for MC + PBO, but negative for IPT-M. This poses an intriguing question: Why is the harm as high in the IPT-M group as the IMI group? Harms are typically viewed as side effects, but collateral effects in RCTs can arise from several sources, including the patient’s indication, the treatment, or their interaction. When pairs of treatments were compared, there were SRD effects for 11 possible clinical situations of the four possible patient outcomes (Table 5).
The values chosen for a study should be highly specific to the context of the disorder and its treatment, in that an overwhelming benefit may cause us to overlook a harm, or a particularly egregious harm may outweigh a substantial benefit. In the clinical setting, clinicians determine for the various scenarios whether the particular harms outweigh benefits and vice versa. This can be accomplished in research by creating a “report card” system for each patient, listing the selected benefits and harms. One hundred pairs of patients should be presented to blinded experts who are then asked to determine which of the two patients has the better outcome. The evaluators will rate if T1>T2, T1=T2, or T1<T2 for each of the 100 pairs. Using a logistic regression model, the preference from the paired differences will be predicted in an integrated preference score (IPS) that can be used to rank-order the patients’ outcomes. Once this is done, the IPS should be validated by conducting the evaluation again with the same experts on another 100 randomized pairs of patients. This method allows investigators to determine what is most important—and unimportant—to clinicians and patients.[24]
This method was used in the SPECTRUM study[25] and further described in other studies.[26–28] The SPECTRUM study[25] (n=291) utilized a panel comprising two psychiatrists expert in the treatment of mood disorders, two nonphysician mental health professionals (one nurse and one social worker) expert in the treatment of mood disorders, one patient with experience of depression, one patient advocate, and one health economist. Two acute treatments were offered in the study (IPT and SSRI) with potentially different profiles of benefit and harm. Benefit was assessed using the Hamilton Rating Scale for Depression (HRSD) and harm was assessed using the Patient-rated Inventory of Side Effects (PRISE). The gender, age, and body mass index (BMI) of patients were assessed at baseline; BMI was re-assessed at 12 weeks. The expert panelists were told to look quickly through the 100 pairs and determine which of the two patients had the better outcome (ties were allowed). The HRSD and PRISE were explained to non-clinician panelists, but no panelist was given specific instructions about how to arrive at their ratings. Panelists had about three weeks to rate 100 pairs of patients.[25]
Logistic regression was used to compute the IPS as follows:
In(p/[1-p])=b0+b1*DH+b2*DP+ b3*DHP, where P=proportion of raters preferring IPT, DH=difference in HRSD slope, DP=difference in the mean PRISE score, and DHP=paired difference between HP products computed for each individual. The calculated integrated preference score can be expressed as: IPSi=0.332–0.66*Hi–0.11*Pi+ 0014*HiPi , where H represents the HRSD slope and P represents the mean of the PRISE. For confirmation purposes, the same panelists were asked to repeat the process with a second set of 100 randomly selected pairs of patients from the same dataset.[25]
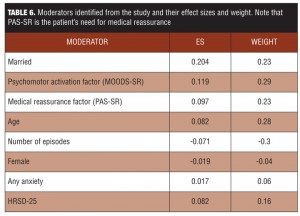
The relationship between the actual and predicted ratings (exploratory and validation samples) using IPS had a correlation of 0.35. This method could be an important and relatively straightforward way of integrating harm and benefit outcomes at the individual patient level. To calculate moderate effect sizes, 32 baseline variables were previously identified as potential moderators. These binary variables were coded +1/2 and -1/2; continuous variables were scaled to a mean of 0 and a variance of 1.[25]
The results were that eight moderators were identified that had both reasonably good effect sizes and were independent (not correlated to each other) (Table 6). These eight moderators were then combined to determine if there were any interactions; their total effect size was 0.31, which is relatively large
(Figure 4).[25]
The effect size was larger for specific patient groups. Using patient profile parameters, it should be possible to select the appropriate patients for a particular therapy. The integrated preference model works well when there is one harm, one benefit, and few variables; it is not clear if this type of analysis would work well on broader studies with multiple harms and benefits.
These exercises demonstrate that an IPS is a practical and useful way of evaluating the outcomes of an RCT. IPS is feasible in simplified studies where there is a single benefit and a single harm, and there is every expectation that it can be used with multiple outcomes, perhaps one IPS based on outcome favored by patient and clinicians, another based on outcomes favored by clinical researchers or basic scientists, and yet another favored by payers or policy makers. Using IPS combined with potential moderators, including pharmacogenetic factors and demographic data, could bring us closer to personalizing medicine.
Conclusion
A consideration of clinically meaningful effect is an important aspect of designing and interpreting any RCT, but can be particularly difficult in CNS trials where effect size may be modest, especially over the short duration of time typical of these trials. The nature of these effect sizes and the ubiquitous importance of human behavior and behavior change leads people from different disciplines to have varied interpretations of what magnitude of effect is clinicallymeaningful, and which outcome measures are most important.
Payers, investors, statisticians, regulators, clinicians, and patients have varied concerns about clinically meaningful effects and may describe their concerns with vastly different terms. However, they share a number of key aspirations for drug development. Among them are new medications that demonstrate clear benefit over existing treatments and that not only treat symptoms, but improve functional ability and quality of life.
The statistical techniques to estimate a clinically meaningful effect are quite different from those used to determine a statistically significant effect, and are in ongoing development.
Future work on treatment effects, including personalized medicine approaches, should consider the use of success rate differences and statistical models that allow for a rational, judicious, and pre-specified use of moderators.
Clinical trial design should be sensitive to the specific concerns of various stakeholders in psychopharmacology in order to allow a full exploration of the impact of new medications, and should take advantage of statistical analyses that can improve the detection of efficacy and safety signals.
Acknowledgments
This manuscript was based on proceedings from the scientific session, “Defining a Clinically Meaningful Effect for the Design and Interpretation of Randomized Controlled Trials,” which was presented during the ISCTM’s 8th Annual Scientific Meeting plus Research-to-Policy Forum, held February 21–23, 2012, in Washington, DC. Dr. Andy Leon, who passed away just days before the meeting took place, spearheaded this session and played the lead role in its development. The authors wish to recognize and honor the memory of Dr. Leon for his commitment to improving the ever-evolving field of CNS?drug development.
The authors would also like to acknowledge Jo Ann LeQuang from LeQ Medical in Angleton, Texas, for her editorial services and Myrna Knaide from M-K Computing in Collegeville, Pennsylvania, for her transcription services.
References
1. Kraemer HC, Kupfer DJ. Size of treatment effects and their importance to clinical research and practice. Biol Psychiatry. 2006;59(11):990–966.
2. Cohen J. Statistical Power Analysis for the Behavioral Sciences. Hillsdale, New Jersey: Lawrence Erlbaum Associates, Inc.; 1977.
3. Appelbaum PS, Roth LH, Lidz CW, et al. False hopes and best data: consent to research and the therapeutic misconception. Hastings Cent Rep. 1987;17(2):20–24.
4. Fisher R. The arrangement of field experiments. J Min Agric Gr Br. 1926;33:505–513.
5. Jaeschke R, Singer J, Guyatt GH. Measurement of health status. Ascertaining the minimal clinically important difference. Control Clin Trials. 1989;10(4):407–415.
6. Lydick E, Epstein RS. Interpretation of quality of life changes. Qual Life Res. 1993;2(3):221–226.
7. Jha AK, Aubert RE, Yao J, et al. Greater adherence to diabetes drugs is linked to less hospital use and could save nearly $5 billion annually. Health Aff (Millwood). 2012;31(8):1836–1846.
8. Sokol MC, McGuigan KA, Verbrugge RR, Epstein RS. Impact of medication adherence on hospitalization risk and healthcare cost. Med Care. 2005;43(6):521–530.
9. Zhu CW, Leibman C, Townsend R, et al. Bridging from clinical endpoints to estimates of treatment value for external decision makers. J Nutr Health Aging. 2009;13(3):256–259.
10. Hurley MV, Walsh NE, Mitchell H, et al. Long-term outcomes and costs of an integrated rehabilitation program for chronic knee pain: a pragmatic, cluster randomized, controlled trial. Arthritis Care Res (Hoboken). 2012;64(2):238–247.
11. Jonsson L, Gerth W, Fastbom J. The potential economic consequences of cognitive improvement with losartan. Blood Press. 2002;11(1):46–52.
12. Wolstenholme JL, Smith SJ, Whynes DK. The costs of treating breast cancer in the United Kingdom: implications for screening. Int J Technol Assess Health Care. 1998;14(2):277–289.
13. Lopez-Pousa S, Vilalta-Franch J, Garre-Olmo J, et al. Effectiveness of donepezil on several cognitive functions in patients with Alzheimer’s disease over 12 months]. Neurologia. 2001 Oct;16(8):342–347.
14. Weinstein MC, Stason WB. Foundations of cost-effectiveness analysis for health and medical practices. N Engl J Med. 1977;296(13):716–721.
15. Baltussen R, Niessen L. Priority setting of health interventions: the need for multi-criteria decision analysis. Cost Eff Resour Alloc. 2006;4:14.
16. National Institute for Health and Clinical Excellence. Depression in adults. Manchester, England: National Institute for Health and Clinical Excellence; 2009 [cited 2013 2 March]; Guidance]. Available from: http://www.nice.org.uk/nicemedia/live/12329/45888/45888.pdf.
17. Leon AC. Comparative effectiveness clinical trials in psychiatry: superiority, noninferiority, and the role of active comparators. J Clin Psychiatry. 2011;72(10):1344–1349.
18. Leucht S, Arbter D, Engel RR, et al. How effective are second-generation antipsychotic drugs? A meta-analysis of placebo-controlled trials. Mol Psychiatry. 2009;14(4):429–447.
19. Meehl P. Theoretical risks and tabular asterisks: Sir Karl, Sir Ronald, and the slow progress of soft psychology. J Consult Clin Py. 1978;46:806–834.
20. Jones L, Tukey J. A sensible formulation of the significance test. Psychol Methods. 2000;5(4):411–414.
21. Baron RM, Kenny DA. The moderator-mediator variable distinction in social psychological research: conceptual, strategic, and statistical considerations. J Pers Soc Psychol. 1986;51(6):1173–1182.
22. National Institute of Mental Health. The Multimodal Treatment of Attention Deficit Hyperactivity Disorder Study (MTA): Questions and Answers. Rockville, MD: National Institute of Mental Health; 2009 [updated November 2009; cited 2013 3 March]; Available from: http://www.nimh.nih.gov/trials/practical/mta/the-multimodal-treatment-of-attention-deficit-hyperactivity-disorder-study-mta-questions-and-answers.shtml.
23. Frank E, Kupfer DJ, Perel JM, et al. Three-year outcomes for maintenance therapies in recurrent depression. Arch Gen Psychiatry. 1990;47(12):1093–1099.
24. Kraemer HC, Frank E, Kupfer DJ. How to assess the clinical impact of treatments on patients, rather than the statistical impact of treatments on measures. Int J Methods Psychiatr Res. 2011;20(2):63–72.
25. Frank E, Cassano GB, Rucci P, et al. Predictors and moderators of time to remission of major depression with interpersonal psychotherapy and SSRI pharmacotherapy. Psychol Med. 2011;41(1):151–162.
26. Kraemer HC, Frank E, Kupfer DJ. How to assess the clinical impact of treatments on patients, rather than the statistical impact of treatments on measures. Int J Methods Psychiatr Res.2011;20:63–72.
27. Frank E, Kupfer DJ, Rucci P, et al. Simultaneous evaluation of the harms and benefits of treatments in randomized clinical trials: demonstration of a new approach. Psychologic Med. 2012;42:865–873.
28. Wallace ML, Frank, E, Kraemer, HC. A novel approach for developing and interpreting treatment moderator profiles in randomized clinical trials. JAMA Psychiatry (in press).