
by Mark E. Whitlock, PhD; Philip W. Woodward, MPhil; and Robert C. Alexander, MD
Dr. Whitlock is BioStatistics Head of Internal Medicine, Early Clinical Development, for Pfizer in Cambridge, United Kingdom. Mr. Woodward is an independent statistics consultant in Newmarket, United Kingdom. Dr. Alexander is with Takeda Pharmaceuticals International Company in Cambridge, Massachusetts.
Funding: No funding was provided.
Disclosures: The authors have no conflicts of interest relevant to the content of this article.
Abstract: Objective: We investigated the accuracy of the often-stated assumption that placebo nonadditivity and an increasing placebo response are major problems in clinical trials and the cause of a trend for smaller treatment effects observed in clinical trials for major depressive disorder (MDD) in recent years. Method of research: We reviewed data from 122 MDD trials conducted between the years 1983 and 2010 (analyzed originally by Undurraga and Baldessarini in 2012) to determine whether the data support the assumption of placebo additivity. Statistical techniques, such as conventional least squares regression, orthogonal least squares regression and locally weighted loess smoothing, were applied to the data set. Results: Re-analysis of the data set showed the active and placebo responses to be highly correlated, to the degree that would be expected assuming placebo additivity, when random variability in both active and placebo response is considered. Despite the placebo responses in MDD trials increasing up to approximately the year 1998, we found no evidence that it has continued to increase since this date, or that it has been the cause of smaller reported treatment effects in recent years. Conclusion: Attempts to reduce the placebo response are unlikely to increase the treatment effect since they are likely to reduce drug nonspecific effects in the treatment arm by a similar amount. Thus, it should come as no surprise that trial designs set up with the sole purpose of reducing placebo response fail to discernibly benefit our ability to identify new effective treatments.
Keywords: Placebo response, placebo additivity, depression, clinical trials, orthogonal regression, antidepressant effects
Innov Clin Neurosci. 2019;16(7–8):12–17
The effect of any treatment is the difference between the response of the patient as a result of getting the treatment and what would have happened to the patient if he or she had not received treatment. What happens to a patient after treatment can be measured, but we cannot directly measure what would have happened to the same patient (in the same time window) if treatment had been denied. This problem is usually addressed in clinical trials by using concurrent controls (i.e., the experimental treatment is studied at the same time as an alternative control, often a placebo). Randomized, placebo-controlled trials (RCTs) have become the gold standard for clinical studies because they allow estimation of the treatment effect relative to placebo and eliminate biases due to differences between trials. For example, in a simple two-arm, parallel-group study with no covariates, the mean treatment effect is measured as the difference between the mean response on treatment and the mean response on placebo.
The implicit assumption in placebo-controlled trials is that the placebo effect is additive. That is, that the effects not attributable to the active drug are equal in both the treatment and placebo arms. A number of papers have questioned the placebo additivity assumption, and, for some drug classes, evidence has been presented that suggests the mechanism of action can interact with placebo mechanisms and result in nonadditivity.1–5 However, the fact remains that, in many disease areas, drug response and placebo response are highly correlated between studies.1
Placebo response is perceived to be a particular problem in the conduct of randomized clinical trials in major depressive disorder (MDD), where the placebo response (change from baseline to endpoint) has been estimated to be approximately 82 percent of the drug response; an estimated 50 percent of placebo-controlled trials with approved antidepressants fail.6–8 Many articles summarizing data in MDD trials suggest that a solution is needed for the problem of high placebo response.9–13 This has resulted in proposed design modifications to reduce the placebo response or the use of clinical trial designs, such as placebo lead-in approaches and sequential parallel comparison design (SPCD), which attempt to increase the treatment effect by removing subjects with a high placebo response.9
We examined data from 122 MDD trials carried out between the years 1983 and 2010. Previous analysis of these trials suggested an increase in placebo response over time that was not matched by an increase in the active response.14 We hypothesized, however, that a more appropriate statistical analysis of the data would not support this conclusion. Other meta-analyses of MDD studies have concluded that the treatment effect is lower in studies with high placebo response.13,15 We believe, however, that although superficially reasonable, it is incorrect to conclude that the treatment effect will be increased by design modifications to reduce the placebo response. This is because such a conclusion ignores the natural random variability in the observed responses that explain this observed correlation and which cannot be designed away.
Placebo and Treatment Responses and Effects
It is important to first clarify the terminology used in this article to assist the reader in better understanding how correlation between observable quantities, often referred to as placebo and treatment “effects,” can occur even when there is, in reality, no correlation between placebo and treatment “true effects.” For example, consider a simple clinical trial in which, after a fixed period of time during which the subjects are given active treatment or placebo, an end-of-study measurement is taken; there are no other covariates to be included in the analysis. In this simple case, the term “estimated placebo response” is defined as the average of the end of study observations from those subjects who received placebo. Clearly, this is something that can be computed and known. “True placebo response,” on the other hand, is the unknowable quantity we are trying to estimate, which represents the conceptual response that would be obtained if we had an infinite number of subjects to study. The estimated and true treatment responses can be defined similarly.
Under the assumption that treatment and placebo effects act independently, “treatment effect” is defined as the difference between the treatment and placebo responses, with “estimated” and “true” treatment effects being defined in a similar way as responses (Figure 1).
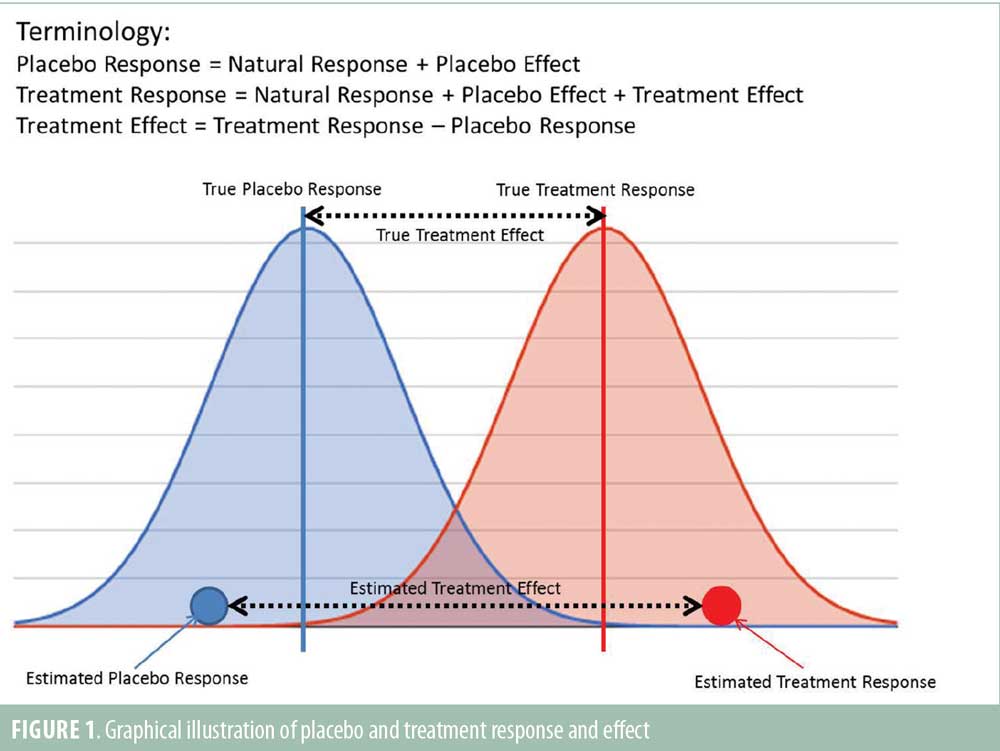
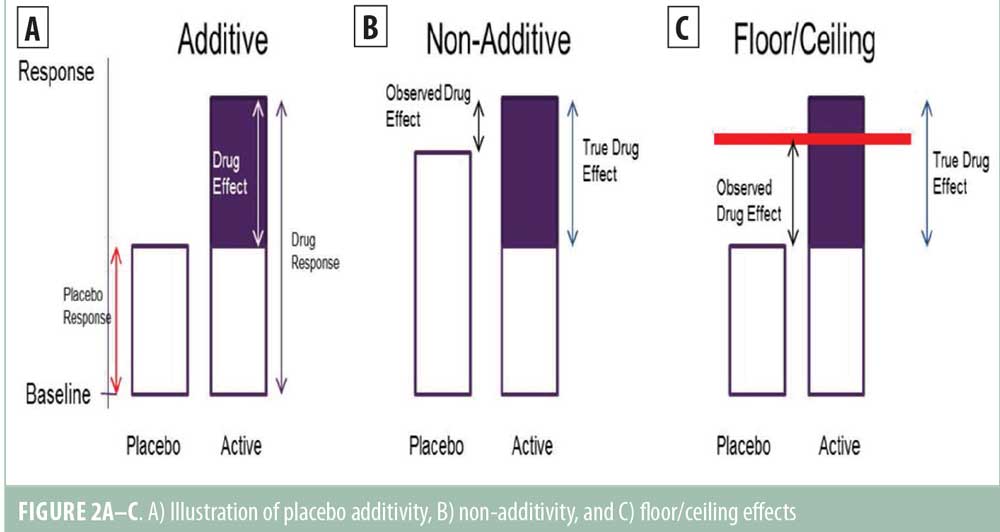
Under the assumption of independence, more typically referred to as placebo additivity, a high placebo response is not necessarily a problem in a clinical trial since it will be associated with a high treatment response (Figure 2a). However, a high placebo response could impact the treatment effect if either of the following occur:
- The placebo effect is different in the placebo and treatment arms. If the placebo effect is higher in the placebo arm than the treatment arm, then the observed treatment effect will be lower than the true treatment effect. (nonadditive, Figure 2b).
- The placebo response is so high (e.g., complete reduction in endpoint measurement) that it limits the available window in which to observe the treatment effect (floor/ceiling effects, Figure 2c). In most well-designed clinical trials, baseline entry criteria should ensure that there is a sufficient window for treatment effects to be observed, even when the placebo response is high, so that floor/ceiling effects are not a common problem.
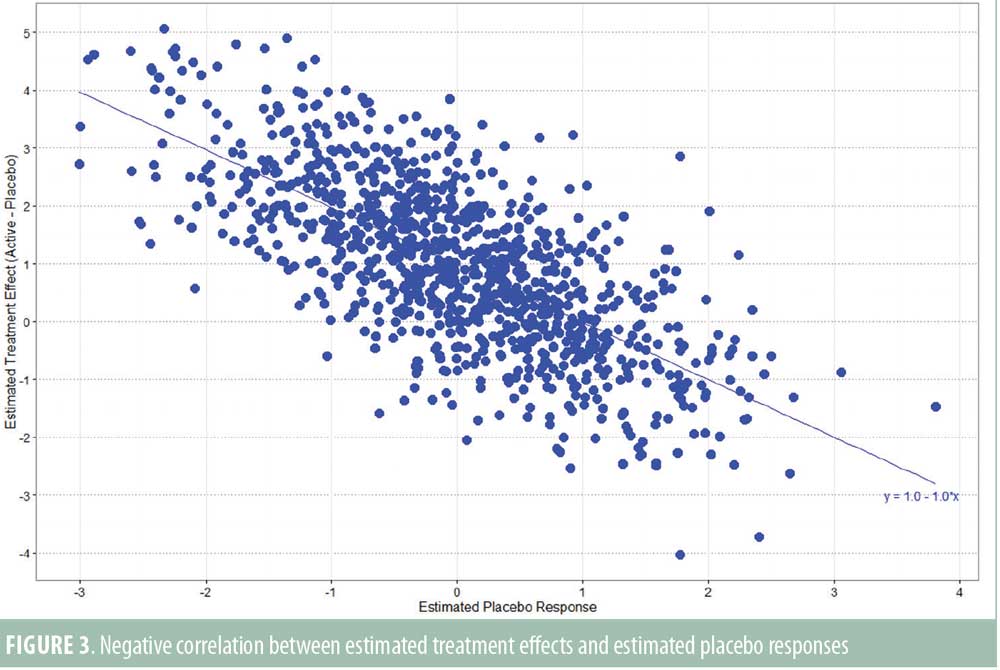
Even when additivity holds, there will still be a negative correlation between the size of the estimated treatment effect and the estimated placebo response. A negative correlation is induced because the treatment effect is calculated by subtracting the placebo response from the treatment response. It is simple to show that if multiple studies were run—all with the same true treatment and placebo responses—and the estimated treatment effects were regressed on the estimated placebo responses, which would vary due to random sampling variation, the true line would have a negative slope of one and an intercept equal to the treatment effect (Figure 3). Even when there is no study-to-study variability in the true treatment and placebo effects, the studies with higher estimated placebo responses, due to random variability, tend to have smaller estimated treatment effects than studies with smaller estimated placebo responses. There is no apparent design solution to this problem (other than increasing the sample size and power) because the studies with a high estimated placebo response relative to the true mean cannot be predicted in advance.
Many measures have been proposed in an attempt to reduce the placebo effect, ranging from improved screening procedures to enable more stringent patient selection, limiting the number of treatment arms, decreasing the length of the study, and reducing the number of visits to design approaches intended to remove or down-weight the impact of subjects with high placebo effect, such as placebo lead-in and SPCD.9,16 These measures might reduce the true mean placebo response, but if the placebo effect is additive, they will not increase the treatment effect since they would also reduce the placebo effect in the treatment arm by an equivalent amount. If placebo additivity holds, then designs that are set up with the sole aim of reducing the placebo response will offer no discernible benefit to the identification of new treatments.
MDD Data Analysis
It has been reported that the superiority of antidepressant medications has been modest relative to placebo and that effect sizes have declined in recent years.14 In a review of antidepressant medication data submitted to the United States Food and Drug Administration (FDA) between 1987 and 1999, Kirsch17 concluded that 80 percent of the responses to medication was duplicated in the placebo control groups, the mean difference between drug and placebo was approximately two points on the Hamilton Depression Rating Scale (HDRS), and that “if drug and placebo effects are additive, the pharmacological effects are clinically negligible.” It also has been suggested that smaller treatment effects in recent years were due to an increase in the placebo response.13,15,18,19 This could only be true if the placebo effect was not additive. Considering this, we investigated the evidence for placebo nonadditivity by examining published data in MDD, a disorder for which there are many approved pharmacological treatments across multiple drug classes.
We re-analyzed data from 122 MDD trials originally analyzed by Undurraga and Baldessarini.14 The search strategy and criteria for selection of these trials are not described here but are well described in the original paper, which provides the trial characteristics and response data for these studies. The outcome measure was categorical response rates for the placebo and treatment groups, defined as at least a 50-percent reduction in initial depression rating-scale scores, typically on the HDRS or Montgomery-Asberg (MADRS) depression scales. Continuous responses for these studies were not presented by the authors of the original review article, who concluded that “a secular increase in sites and participants per trial was associated, selectively, with rising placebo associated response rates, resulting in declining drug–placebo contrasts or effect-size.”
In the current article, we re-analyzed the relationship between both placebo response rate versus year and active response rate versus year, fitting a locally weighted loess smoothing line to the data (Figure 4).20 Our interpretation of results is that both placebo responder rates and active responder rates increased up to approximately 1998. This is consistent with the results reported by Walsh,21 who concluded that “response to placebo has increased significantly in recent years, as has the response to medication.”
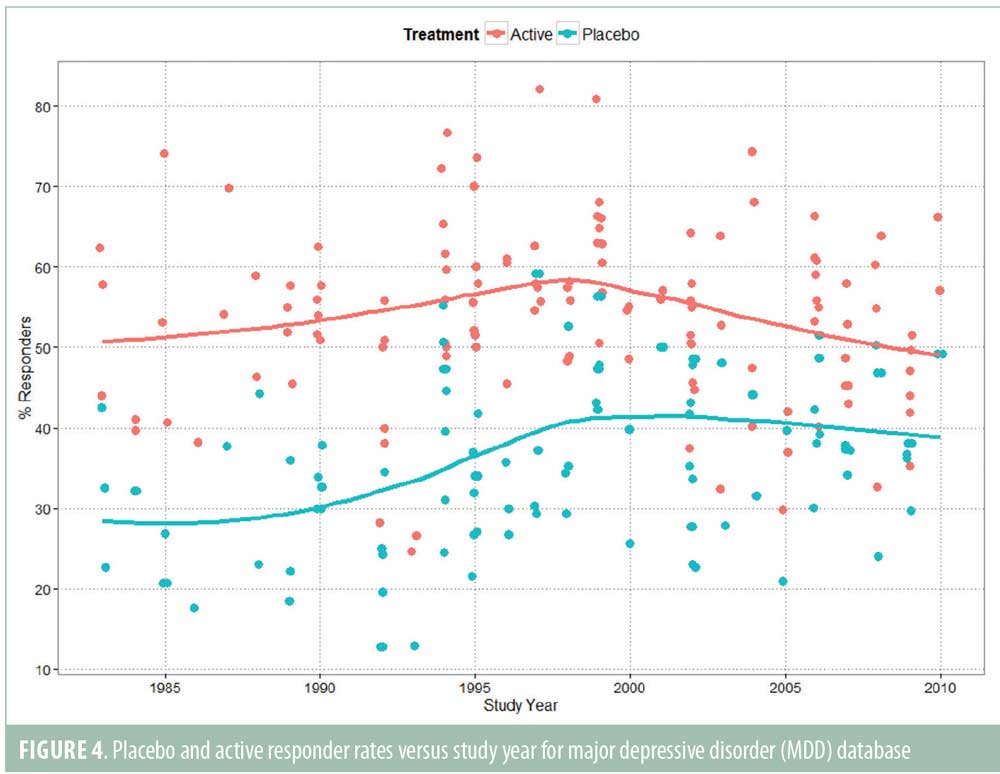
We identified no noticeable increase in the average placebo response since 1998, although we observed a trend for smaller treatment response rates. This conclusion is similar to that of Furukawa et al,22 who reported that placebo response rates in antidepressant trials have remained consistently within the range of 35 to 40 percent since the year 1991, although our results differed in the estimate of the year at which the increase in placebo response leveled off. This difference might be due to the wider range of studies examined by Furukawa et al, which included unpublished data submitted to the FDA.
The analysis in Figure 4 combines multiple compound classes from different time periods, which might make the interpretation of the trends in treatment effects more difficult. To investigate this further, we analyzed the same data stratified by compound class. Studies with MAOIs were excluded due to limited data within this class (Figure 5). A locally weighted loess smoothing line was fitted to the data from each drug class separately, showing, within each class of drug, a correlation between placebo and/or active response (i.e., additivity). Trends for increases or decreases in the placebo and active responder rates tend to mirror each other, although it is apparent that a trend for smaller treatment effects in recent years with selective serotonin reuptake inhibitors (SSRI) and serotonin-norepinephrine reuptake inhibitor (SNRI) compounds are not associated with increases in the placebo response.
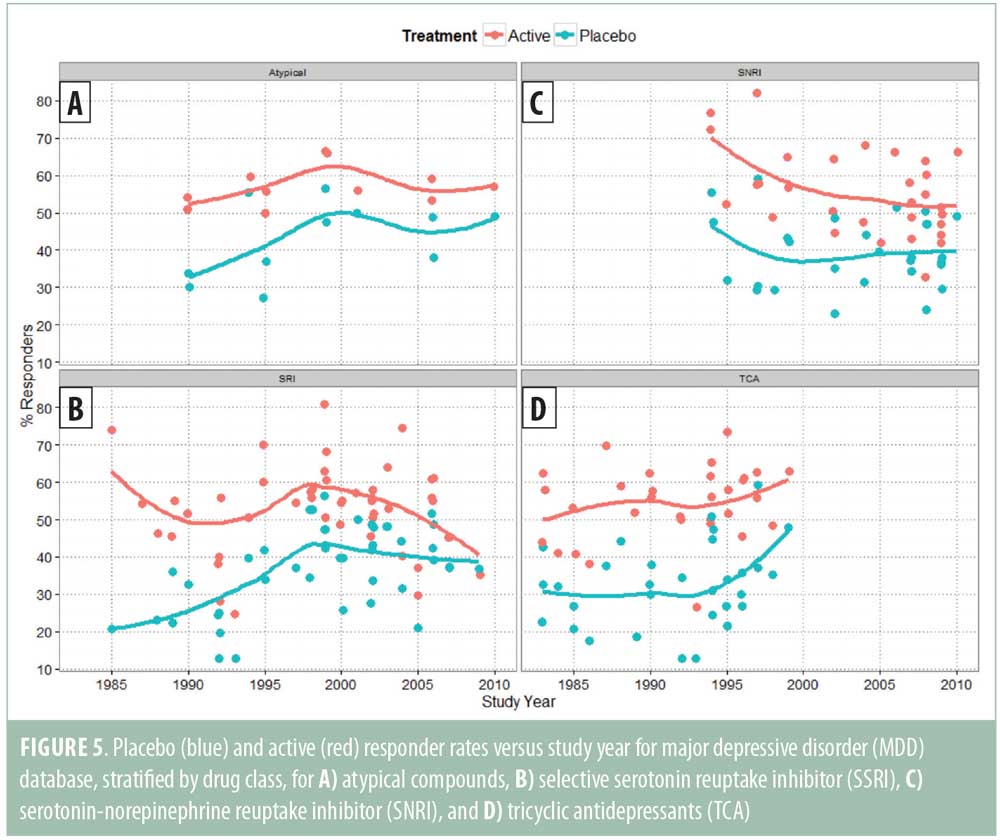
Additionally, we examined the correlation between active and placebo responder rates in the 122 MDD studies (Figure 6). To model the relationship between the two, one could fit an ordinary least squares regression line, but this approach only minimizes squared residuals in the y-direction, which would lead to the fitted line: Active responder rate = 31.7% + 0.6*Placebo responder rate. The slope of 0.6 suggests that as the placebo response increases, the active response does not increase at the same rate (i.e., only partial additivity). This is equivalent to the findings reported elsewhere, when, after dividing the estimated placebo response rates into bins of 20 percent or less, 20 to 30 percent, 30 to 40 percent, and 40 percent or greater, the difference between active response rates and placebo response rates were shown to progressively shrink.13,15 The decrease in estimated treatment effects at higher estimated placebo rates should be expected and does not mean that placebo effects are nonadditive since it can be explained by the inherent negative correlation between treatment effect and placebo response, as previously discussed. An ordinary least squares regression analysis is flawed because it ignores the random variability in both placebo and active response rates. The variability in both active and placebo response rates in the 122 studies is a mixture of between-study variability in the true responder rates and within-study variability in the estimated response rates.
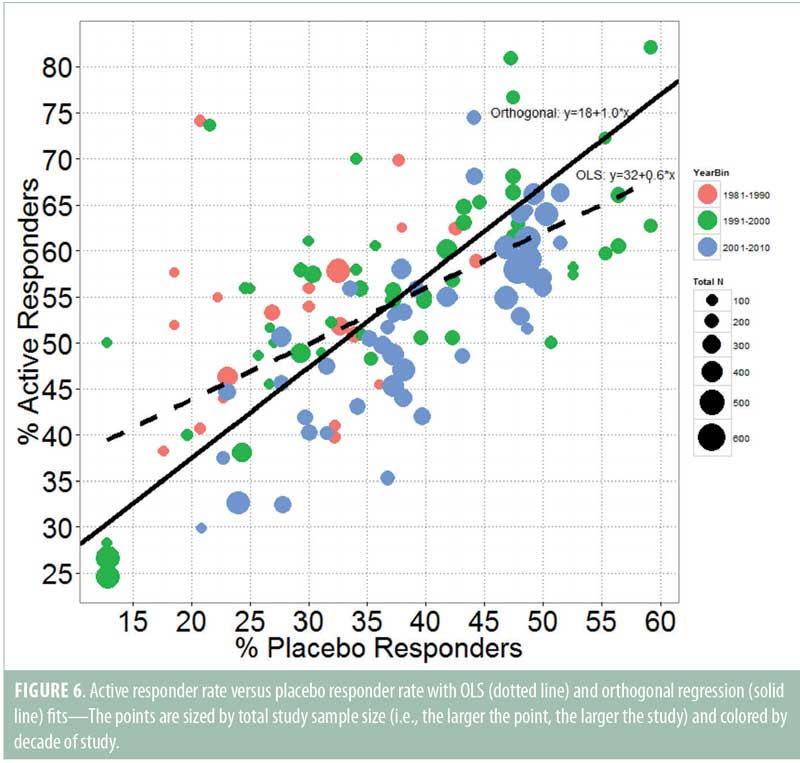
A more appropriate analysis of the relationship between active and placebo responder rate would be to fit the regression line using orthogonal regression.23 This minimizes the sum of squared residuals orthogonal to the fitted line and is more appropriate since both the y (active response) and x (placebo response) variables are subject to random variability. The variability is assumed equal in both variables. An orthogonal least squares regression line fit gives the fitted regression line: Active responder rate = 17.7% + 1.0*Placebo responder rate. The slope of 1.0 (standard error=0.12) suggests that any increase in placebo response is associated with an equivalent increase in active response and that the average treatment effect (difference in responder rates) is approximately 18 percent across the placebo response range studied. Clearly, the fitted slope of exactly 1.0 strongly supports the assumption of placebo additivity on this scale.
The points in Figure 6 were colored by decade of study and sized by total study sample size to highlight two additional features. First, the majority of the more recent studies reported between the years 2001 and 2010 (in blue) tend to lie below the fitted orthogonal regression line. That is, they tend to have smaller active responder rates for a given placebo responder rate than the earlier studies. Importantly, this is true even in studies with low placebo response, again suggesting that treatment effects have decreased in recent years, but not because of an increasing placebo response. The point size also shows that recent studies tended to have larger sample sizes. The trend for larger studies in recent years and for the larger studies to have smaller treatment effects was the conclusion reached by Undurraga and Baldessarini14 and supported by our analysis.
Investigating the possible causes for the reported smaller treatment effects in recent years is outside the scope of the current analysis. However, given the relationship between active and placebo response revealed by the orthogonal regression fit, we found no evidence attributing this to higher placebo response rates or supporting that the placebo effect is nonadditive.
Discussion
When the natural variability in both active and placebo responses is appropriately accounted for, there is strong, data-driven evidence that the assumption of placebo additivity holds for the 122 MDD trials we analyzed. Orthogonal regression is a more appropriate analysis of the relationship between active and placebo responder rates since there is (assumed equal) variability in both measurements. Using this method, the fitted slope of exactly 1.0 when regressing active responder rate against placebo responder rate shows the data to be entirely consistent with the placebo additivity assumption. This is not to say that a high placebo response in an individual trial is not a problem—even if placebo effects are additive, random variability in the observed response will cause negative correlation between the size of the estimated treatment effect and the estimated placebo response. However, the implication of placebo additivity is that design approaches intended primarily to reduce the true mean placebo effect are likely to affect the active and placebo responses equally; hence, they will be unsuccessful at increasing the treatment effect. This might explain why placebo lead-in designs generally have not been considered successful. Placebo lead-in phases are often used to screen out patients who have a relatively high response during a (typically single-blinded) placebo lead-in phase. External reviews of the results of placebo lead-in designs have concluded that although the placebo response is numerically lower compared to studies without a placebo lead-in phase, there is little evidence of success in increasing the treatment effect.21,24–26 This has been attributed to bias due to nonblinded clinicians and random variability in placebo response resulting in inclusion/exclusion of subjects who are not consistent placebo responders. Both of these are valid reasons, but an alternative explanation for lack of success of placebo lead-ins is that if the placebo effect is additive, removing subjects with high placebo response will have the same effect (in a randomized trial) on both the active and placebo groups and hence have no benefit to the treatment effect. Thus, we should not be surprised if other designs that are set up with the sole aim of reducing the placebo response fail to show any discernible benefit on our ability to identify new treatments.
Several meta-analyses have indicated that baseline depression severity influences antidepressant treatment response in RCTs.17,27,28 This has been cited as evidence supporting the theory that placebo response is not additive in depression trials with decreased responsiveness to placebo in patients with severe depression. While independent analyses support larger antidepressant/placebo differences in study subjects with more severe depression, the reason for this difference varies between studies. Kirsch et al17 reported less placebo change in patients with more severe depression, but Khan et al27 found no change in placebo response but greater antidepressant response in patients with severe depression. Fournier et al28 also reported greater antidepressant response in patients with severe depression, but also found a small positive relationship between baseline severity and placebo response. Thus, is it unclear if placebo response really changes with increasing baseline severity or if drug effects alone increase in patients with more severe depression.
The perception that studies are failing because of an increasing placebo response and placebo nonadditivity is not limited to MDD trials. High placebo response has been reported in other therapeutic areas including pain,31 schizophrenia,32–34 and irritable bowel syndrome.35 In epilepsy, Rheims et al29 reported a meta-analysis of adjunctive-therapy trials in partial epilepsy and concluded that the “increase in response to placebo during the last two decades was clearly associated with a parallel increase in response to active medication.” Yet, it is our experience that this increase in placebo response is still interpreted as a problem that needs a solution.30 Our analysis of MDD trials suggests that further investigation is warranted in these other treatment areas.
More focus on study variables and methods of analysis that provide greater diagnostic precision in measurement might yield better, more accurate results. For example, given the vast amount of historical data in this area, we believe greater use of Bayesian methods to formally utilize this information should be adopted (e.g., through the use of an informative prior for the placebo response). Not only will this allow researchers to run smaller studies with the obvious benefits of lower cost and less time to next decision point, as well as greater precision with the same sized studies, but it should also benefit recruitment rates and patient selection quality due to more efficient designs that can randomize more patients to treatment arms that have greater potential for improved outcomes.
Limitations. A limitation of our analysis is its restriction to data from published studies up to 2010. Unpublished studies and data from studies after 2010 were not included in our analyses. However, the majority of the publications that support theories on the lack of additivity in drug effects are based on analyses of the same published data that we analyzed in our review. Furukawa et al22 reached a similar conclusion of a stable placebo response rate since the early 1990s using a wider range of studies, including unpublished data. Given the overlap between the studies included in Furukawa’s analysis and our own, it is unlikely our conclusion about placebo additivity would change. Our primary aim was to demonstrate that by using a more appropriate statistical analyses of these data, the widely reported conclusions regarding placebo nonadditivity and the need for trial design solutions that reduce placebo effect are not supported.
Conclusion
Placebo response is an important issue in clinical drug trials; however, our observation that the treatment and placebo effects observed in MDD trials are highly correlated, to the degree expected under the assumption of placebo additivity, indicates that perhaps the recent focus on designing trials that reduce placebo response and/or attempt to remove high placebo responders could be ineffective. Rather, other factors, such as better patient selection and diagnostic accuracy, enhanced rater training site, certification and monitoring, use of new efficacy scales with better psychometric characteristics, more care in the monitoring of treatment adherence, increased ratio of subjects/site, and reduced enrollment pressure, should take precedence over reducing placebo response when designing better drug trials.36,37
References
- Kirsch I. Are drug and placebo effects in depression additive? Biol Psychiatry. 2000;47:733–773.
- Fountoulakis K, Moller HJ. Antidepressant drugs and the response in the placebo group: the real problem lies in our understanding of the issue. J Psychopharmacol. 2012;26(5):744–750.
- Enck P, Klosterhalfen S. The placebo response in clinical trials—the current state of play. Complement Ther Med. 2013;21:98–101.
- Eippert F, Bingel U, Schoell ED, et al. Activation of the opioidergic descending pain control system underlies placebo analgesia. Neuron. 2009;63:533–543.
- Petrovic P, Kalso E, Petersson KM, et al. A prefrontal non-opioid mechanism in placebo analgesia. Pain. 2010;150:59–65.
- Kirsch I. The emperor’s new drugs: medication and placebo in the treatment of depression. Handb Exp Pharmacol. 2014;225:291–303.
- Laughren TP. The scientific and ethical basis for placebo-controlled trials in depression and schizophrenia: an FDA perspective. Eur Psychiatry. 2001;16(7):418–423.
- Khan A, Khan S, Brown WA. Are placebo controls necessary to test new antidepressants and anxiolytics? Int J Neuropsychophamacol. 2002;5(3):193–197.
- Fava M, Evins AE, Dorer DJ et al. The problem of the placebo response in clinical trials for psychiatric disorders: culprits, possible remedies, and a novel study design approach. Psychother Psychosom. 2003;72(3):115–127.
- Lakoff A. The right patients for the drug: managing the placebo effect. Biosocieties. 2007;2(1):57–73.
- Merlo-Pich E, Alexander RC, Fava M, et al. A new population-enrichment strategy to improve efficiency of placebo-controlled clinical trials of antidepressant drugs. Clin Pharmacol Ther. 2010;88:634–642.
- Iovieno N, Papakostas GI. Correlation between different levels of placebo response rate and clinical trial outcome in major depressive disorder: a meta-analysis. J Clin Psychiatry. 2012;73(10):1300–1306.
- Papakostas GI, Ostergaard SD, Iovieno N. The nature of placebo response in clinical studies of major depressive disorder. J Clin Psychiatry. 2015;76(4):456–466.
- Undurraga J, Baldessarini RJ. Randomized, placebo-controlled trials of antidepressants for acute major depression; thirty-year meta-analytic review. Neuropschopharmacology. 2012;37:851–864.
- Iovieno N, Papakostas GI. Correlation between different levels of placebo response rate and clinical trial outcome in major depressive disorder: a meta-analysis. J Clin Psychiatry. 2012;73(10):1300–1306.
- Schatzberg AF, Kraemer HC. Use of placebo control groups in evaluating efficacy of treatment of unipolar major depression. Biol Psychiatry. 2000;47(8):736–744.
- Kirsch I, Moore TJ, Scoboria A, Nicholls SS. The emperor’s new drugs: An analysis of antidepressant medication data. Prevention and Treatment. 2002;5:Article 23.
- Khin NA, Chen YF, Yang Y, et al. Exploratory analysis of efficacy data from major depressive disorder trials submitted to the US Food and Drug Administration in support of new drug applications. J Clin Psychiatry. 2011;72(4):464–472.
- Rutherford BR, Roose SP. A model of placebo response in antidepressant clinical trials. Am J Psychiatry. 2013;170(7):723–733.
- Cleveland WS. Robust locally weighted regression and smoothing scatterplots. J Am Stat Assoc. 1979;74(368):829–836.
- Walsh BT, Seidman SN, Sysko R, et al. Placebo response in studies of major depression: variable, substantial, and growing. JAMA. 2002;287(14):1840–1847.
- Furukawa T, Cipriani A, Atkinson L, et al. Placebo response rates in antidepressant trials: a systematic review of published and unpublished double-blind randomised controlled studies. Lancet Psychiatry. 2016;3:1059–1066.
- Mandel J. Fitting straight lines when both variables are subject to error. Journal of Quality Technology. 1984;16:1–14.
- Chen YF, Yang Y, Hung HJ, et al. Evaluation of performance of some enrichment designs dealing with high placebo response in psychiatric clinical trials. Contemp Clin Trials. 2011;32:592–604.
- Trivedi MH, Rush J. Does a placebo run-in or a placebo treatment cell affect the efficacy of antidepressant medications? Neuropsychopharmacology. 1994;11(1):33–43.
- Lee S, Walker JR, Jakul L, et al. Does elimination of placebo responders in a placebo run-in increase the treatment effect in randomized clinical trials? A meta-analytic evaluation. Depress Anxiety. 2004;19:10–19.
- Khan A, Leventhal RM, Khan SR, et al. Severity of depression and response to antidepressants and placebo: an analysis of the Food and Drug Administration database. J Clin Psychopharmacol. 2002;22(1):40–45.
- Fournier JC, DeRubeis RJ, Hollon SD, et al. Antidepressant drug effects and depression severity: a patient-level meta-analysis. JAMA. 2010;303:47–53.
- Rheims S, Perucca E, Cucherat M, et al. Factors determining response to antiepileptic drugs in randomized controlled trials. A systematic review and meta-analysis. Epilepsia. 2011;52:219–233.
- Friedman D, French JA. Clinical trials for therapeutic assessment of antiepileptic drugs in the 21st century: obstacles and solutions. Lancet Neurol. 2012;11:
827–834. - Tuttle AH, Tohyama S, Ramsay T, et al. Increasing placebo responses over time in U.S. clinical trials of neuropathic pain. Pain. 2015;156:2616–2626.
- Kemp AS, Schooler NR, Kalali AH, et al. What is causing the reduced drug-placebo difference in recent schizophrenia clinical trials and what can be done about it? Schizophr Bull. 2008;36:504–509.
- Chen YF, Wang SJ, Khin NA, et al. Trial design issues and treatment effect modeling in multiregional schizophrenia trials. Pharm Stat. 2010;9:217–229.
- Alphs L, Benedetti F, Fleischhacker WW, et al. Placebo-related effects in clinical trials in schizophrenia: what is driving this phenomenon and what can be done to minimize it? Int J Neuropsychopharmacol. 2012;15(7):1003–1014.
- Shah E, Pimentel M. Placebo effect in clinical trial design for irritable bowel syndrome. J Neurogastroenterol Motility. 2014;20:163–170.
- Kobak KA, Feiger AD, Lipsitz JD. Interview quality and signal detection in clinical trials. Am J Psychiatry. 2005;162(3):628.
- McCann D, Petry N, Bresell A, et al. Medication nonadherence, “professional subjects,” and apparent placebo responders: overlapping challenges for medications development. J Clin Psychopharmacol. 2015;35(5):1–8.





